Fluid Dynamics- 1🤹🏻♂️
- Taliya Mammadhasanzada

- Aug 19, 2020
- 6 min read
Updated: Aug 19, 2020
Warm greetings to all🤩 in the 16th post on #Day16 ! Today, we will start writing about Fluid Dynamics 😉. In this series of posts, we will learn about✨:
Bernoulli equation
Laminar flow
Turbulent flow
Newton's second law along a streamline
Static, Stagnation, Dynamic and Total pressure
Summary
Here we go 🚜,
Newton's Second Law along a streamline🖇
In this post, we consider the motion of inviscid fluids. That is, the fluid is assumed to have zero viscosity. If the viscosity is zero, then the thermal conductivity of the fluid is also zero and there can be no heat transfer (except by radiation). In practice there are no inviscid fluids, since every fluid supports shear stresses when it is subjected to a rate of strain displacement. For many flow situations the viscous effects are relatively small compared with other effects. As a first approximation for such cases it is often possible to ignore viscous effects. For example, often the viscous forces developed in flowing water may be several orders of magnitude smaller than forces due to other influences, such as gravity or pressure differences. For other water flow situations, however, the viscous effects may be the dominant ones. Similarly, the viscous effects associated with the flow of a gas are often negligible, although in some circumstances they are very important. We assume that the fluid motion is governed by pressure and gravity forces only and examine Newton’s second law as it applies to a fluid particle in the form:
📌(Net pressure force on particle) + (net gravity force on particle)=(particle mass)*(particle acceleration)
As the particle moves about, it follows a particular path, the shape of which is governed by the velocity of the particle. The location of the particle along the path is a function of where the particle started at the initial time and its velocity along the path. If it is steady flow (i.e., nothing changes with time at a given location in the flow field), each successive particle that passes through a given point [such as point (1) in Fig. 3.1a] will follow the same path. For such cases the path is a fixed line in the x–z plane. Neighboring particles that pass on either side of point (1) follow their own paths, which may be of a different shape than the one passing through (1). The entire x–z plane is filled with such paths.

For steady flows each particle slides along its path, and its velocity vector is everywhere tangent to the path. The lines that are tangent to the velocity vectors throughout the flow field are called streamlines. For many situations it is easiest to describe the flow in terms of the “streamline” coordinates based on the streamlines as are illustrated in Fig. 3.1b. The particle motion is described in terms of its distance s=s(t), along the streamline from some convenient origin and the local radius of curvature of the streamline R=R(s). The distance along the streamline is related to the particle’s speed by V=ds/dt and the radius of curvature is related to the shape of the streamline. In addition to the coordinate along the streamline, s, the coordinate normal to the streamline, n, as is shown in Fig. 3.1b, will be of use
🧨Note: Fluid particles accelerate normal to and along streamlines!

This is the celebrated Bernoulli equation—a very powerful tool in fluid mechanics. In 1738 Daniel Bernoulli published his Hydrodynamics in which an equivalent of this famous equation first appeared. To use it correctly we must constantly remember the basic assumptions used in its derivation:
viscous effects are assumed negligible,
the flow is assumed to be steady,
the flow is assumed to be incompressible, and
the equation is applicable along a streamline.
In the derivation of equation above, we assume that the flow takes place in a plane (the x–zplane). In general, this equation is valid for both planar and nonplanar (three-dimensional) flows, provided it is applied along the streamline.
Derivation of Bernoulli equation🖇
Mechanism of fluid flow is a complex process. However, it is possible to get some important properties with respect to streamline flows by using the concept of conservation of energy. Let us take an example of any fluid moving inside a pipe. The pipe has different cross-sectional areas in different parts and is present in different heights. Refer to the diagram below.
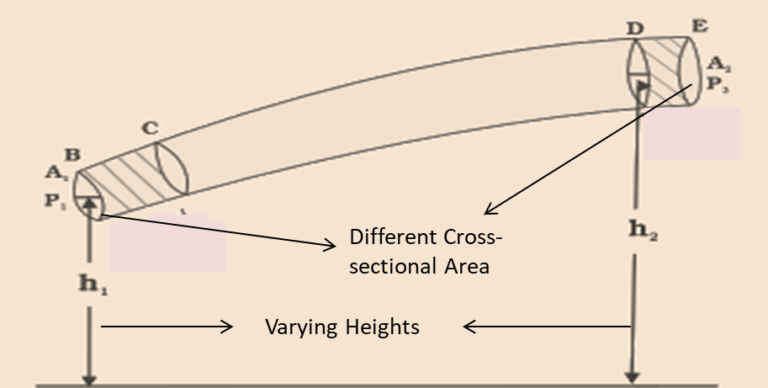
Now we will consider that an incompressible fluid will flow through this pipe in a steady motion. As per the concept of the equation of continuity, the velocity of the fluid should change. However, to produce acceleration, it is important to produce a force. This is possible by the fluid around it but the pressure must vary in different parts.
Bernoulli’s equation is the general equation that describes the pressure difference in two different points of pipe with respect to velocity changes or change in kinetic energy and height changes or change in potential energy.
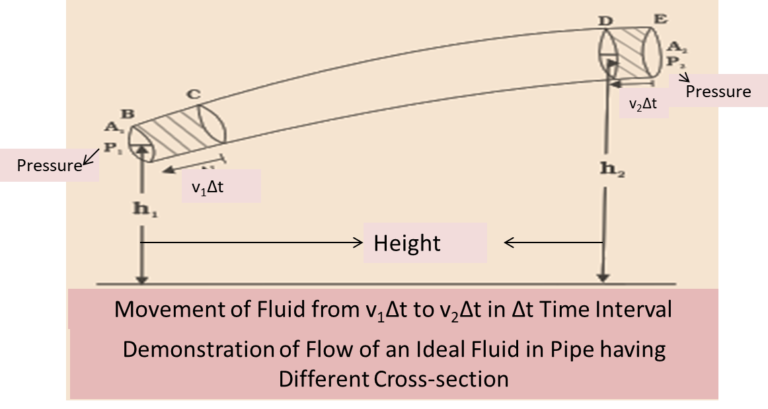
Let us consider two different regions in the above diagram. Let us name the first region as BC and the second region as DE. Now consider the fluid was previously present in between B and D. However, this fluid will move in a minute (infinitesimal) interval of time (∆t).
If the speed of fluid at point B is v1 and at point D is v2. Therefore, if the fluid initially at B moves to C then the distance is v1∆t. However, v1∆t is very small and we can consider it constant across the cross-section in the region BC.
📌Similarly, during the same interval of time ∆t the fluid which was previously present in the point D is now at E. Thus, the distance covered is v2∆t. Pressures, P1 and P2, will act in the two regions, A1 and A2, thereby binding the two parts. The entire diagram will look something like the figure given below.
Finding the Work Done✨
First, we will calculate the work done (W1) on the fluid in the region BC. Work done is
W1 = P1*A1*(v1∆t) = P1*∆V
Moreover, if we consider the equation of continuity, the same volume of fluid will pass through BC and DE. Therefore, work done by the fluid on the right-hand side of the pipe or DE region is
W2 = P2*A2*(v2∆t) = P2*∆V
Thus, we can consider the work done on the fluid as – P2∆V. Therefore, the total work done on the fluid is
W1 – W2 = (P1 − P2)*∆V
The total work done helps to convert the gravitational potential energy and kinetic energy of the fluid. Now, consider the fluid density as ρ and the mass passing through the pipe as ∆m in the ∆t interval of time.
Hence,
∆m = ρ*A1*v1∆t = ρ*∆V
Change in Gravitational Potential and Kinetic Energy✨
Now, we have to calculate the change in gravitational potential energy ∆U.

Similarly, the change in ∆K or kinetic energy can be written as
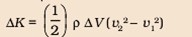
Calculation of Bernoulli’s Equation✨
Applying work-energy theorem in the volume of the fluid, the equation will be

Dividing each term by ∆V, we will obtain the equation

Rearrangement

The above equation is the Bernoulli’s equation. However, the 1 and 2 of both the sides of the equation denotes two different points along the pipe. Thus, the general equation can be written as
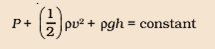
Thus, we can state that Bernoulli’s equation state that the Pressure (P), potential energy (ρgh) per unit volume and the kinetic energy (ρ*v2/2) per unit volume will remain constant.
Important Points to Remember✨
It is important to note that while deriving this equation we assume there is no loss of energy because of friction if we apply the principle of energy conservation. However, there is actually a loss of energy because of internal friction caused during fluid flow. This, in fact, will result in the loss of some energy.
🧨Note: Watch this video- Bernoulli's principle: https://www.youtube.com/watch?v=UJ3-Zm1wbIQ
References📖
Fundamentals of Fluid Mechanics by Bruce R. Munson 7th edition
https://www.toppr.com/guides/physics/mechanical-properties-of-fluids/bernoullis-principle/
Introduction to Fluid mechanics/Edward J. Shaughnessy, Ira M. Katz, James P. Schaffer.
Additional Resources 🧪🔑
You can get deep insight about Process/Chemical Engineering from these sources😉:
https://coursemania.xyz/course.html?id=433291- Free course on Fundamentals of Fluid Mechanics
https://t.me/ebookstorage/178- Engineering Heat Transfer
https://t.me/ebookstorage/159- Fundamentals of Engineering Thermodynamics (9th Edition) (2018)
https://t.me/ebookstorage/183-Heat Transfer applications and principles
https://t.me/ebookstorage/171-Design and Operation of Heat Exchangers and their Networks (2020)
https://t.me/ebookstorage/215- Industrial Separation Processes (book)
https://t.me/ebookstorage/214- Advanced Process Engineering Control (book)
https://t.me/OilAndGas- Information about Oil&Gas (mainly arabic lang)
https://t.me/chemical_worlds- Chemical Engineering Books, Quizzes and GATE Study Group
https://t.me/chemical_environmental- Discussion group related to Chemical Engineering Problems
https://t.me/chemicalengineeringworld_cew- Everything related to Chemical Engineering
https://t.me/ebookgate- Chemical Engineering E-books (Telegram Channel)
https://www.youtube.com/channel/UCqioh32NOJc8P7cPo3jHrbg- Piping Analysis
https://www.youtube.com/channel/UCQfMyugsjrVUWU0v_ZxQs2Q -Mechanics of engineered devices
http://chemicalengineeringguy.com/- suggests a wide range of courses in Chemical engineering (you can find free courses on topic of Aspen HYSYS, Aspen Plus)
https://www.youtube.com/user/LearnEngineeringTeam- suggests working principles of every engineered devices, equipment and etch.
https://www.youtube.com/channel/UCR0EfsRZIwA5TVDaQbTqwEQ- suggests great information about pumps, compressors with animation.
Today we have begun learning about Fluid Dynamics part 1. Now, time to say goodbye👋🏻 until tomorrow and Stay tuned for more content 😉🌝✨!
✏️Note: If you need one of those books or links, you can contact me via my email or LinkedIn profile.
#process #processengineering #engineering #chemical #chemicalengineering #technical #education #dailypost #newpost #wixsite #day15 #technology #material #materialbalance #mass #massbalance #project #projectengineering #selfdevelopment #challenge #recycle #streams #purge #improvement #fluidflow #flow #fluidmechanics #fluiddynamics #water #waterhammer #contuinity #energy #equations #Pfd #processdiagrams #diagrams #piping #instrumentation #pid #development #examples #study #studentlife #fluidstatics



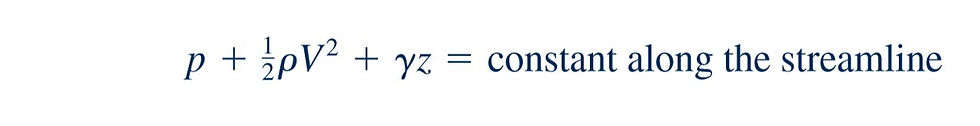
Comments