top of page
Search
Writer's pictureTaliya Mammadhasanzada
Aug 20, 20205 min read

Fluid Dynamics 2🦦

Warm greetings to all🤩 in the 17th post on #Day17 ! Today, we will resume the 2nd part of Fluid Dynamics. Here we go 🧙🏻‍♀️,



Static, Stagnation, Dynamic and Total Pressure👻

A useful concept associated with the Bernoulli equation deals with the stagnation and dynamic pressures. These pressures arise from the conversion of kinetic energy in a flowing fluid into a “pressure rise” as the fluid is brought to rest. In this section we explore various results of this process. Each term of the Bernoulli equation,



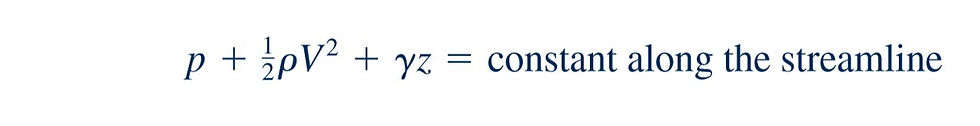
has the dimensions of force per unit area—psi, The first term, p, is the actual thermodynamic pressure of the fluid as it flows. To measure its value, one could move along with the fluid, thus being “static” relative to the moving fluid. Hence, it is normally termed the static pressure. The third term in Equation, is termed the hydrostatic pressure, in obvious regard to the hydrostatic pressure variation. It is not actually a pressure but does represent the change in pressure possible due to potential energy variations of the fluid as a result of elevation changes. The second term in the Bernoulli equation, is termed the dynamic pressure. Its interpretation can be seen in Fig. 3.4



by considering the pressure at the end of a small tube inserted into the flow and pointing upstream. After the initial transient motion has died out, the liquid will fill the tube to a height of H as shown. The fluid in the tube, including that at its tip, (2), will be stationary. That is, V (2) is 0, point (2) is a stagnation point. If we apply the Bernoulli equation between points (1) and (2), using V(2)=0 and assuming that z1=z2 we find that :


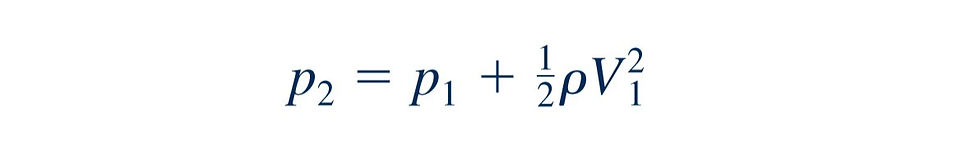
Check also this pic: (Fig. 3.5)


Hence, the pressure at the stagnation point is greater than the static pressure, p1, by p*(v1)^2 the dynamic pressure.

It can be shown that there is a stagnation point on any stationary body that is placed into a flowing fluid. Some of the fluid flows “over” and some “under” the object. The dividing line (or surface for three-dimensional flows) is termed the stagnation streamline and terminates at the stagnation point on the body. For symmetrical objects (such as a baseball) the stagnation point is clearly at the tip or front of the object as shown in Fig. 3.5a. For other flows such as a water jet against a car as shown in Fig. 3.5b, there is also a stagnation point on the car.

If elevation effects are neglected, the stagnation pressure,

  • p+ p*V^2/2,

is the largest pressure obtainable along a given streamline. It represents the conversion of all of the kinetic energy into a pressure rise. The sum of the static pressure, hydrostatic pressure, and dynamic pressure is termed the total pressure, p(T). The Bernoulli equation is a statement that the total pressure remains constant along a streamline. That is,



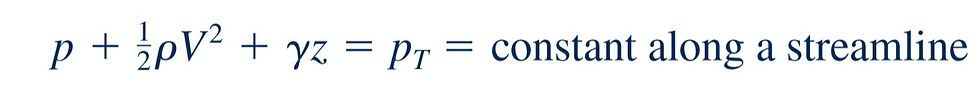
Again, we must be careful that the assumptions used in the derivation of this equation are appropriate for the flow being considered.

Cavitation🧠

In general, an increase in velocity is accompanied by a decrease in pressure. For example, the velocity of the air flowing over the top surface of an airplane wing is, on the average, faster than that flowing under the bottom surface. Thus, the net pressure force is greater on the bottom than on the top—the wing generates a lift. If the differences in velocity are considerable, the differences in pressure can also be considerable. For flows of gases, this may introduce compressibility effects as discussed in previous posts. For flows of liquids, this may result in cavitation, a potentially dangerous situation that results when the liquid pressure is reduced to the vapor pressure and the liquid "boils".


 

Simply defined, cavitation is the formation of bubbles or cavities in liquid, developed in areas of relatively low pressure around an impeller. The imploding or collapsing of these bubbles trigger intense shockwaves inside the pump, causing significant damage to the impeller and/or the pump housing.

If left untreated, pump cavitation can cause:

  • Failure of pump housing

  • Destruction of impeller

  • Excessive vibration - leading to premature seal and bearing failure

  • Higher than necessary power consumption

  • Decreased flow and/or pressure

There are two types of pump cavitation: suction and discharge.

❗️We will talk further details later.


Flowrate Measurement 🧚🏻

Many types of devices using principles involved in the Bernoulli equation have been developed to measure fluid velocities and flowrates. The Pitot-static tube is an example. Other examples discussed below include devices to measure flowrates in pipes and conduits and devices to measure flowrates in open channels. Here we will consider “ideal” flowmeters—those devoid of viscous, compressibility, and other “real-world” effects. Our goal here is to understand the basic operating principles of these simple flowmeters. An effective way to measure the flowrate through a pipe is to place some type of restriction within the pipe as shown in Fig. 3.18



and to measure the pressure difference between the low-velocity, high-pressure upstream section (1) and the high-velocity, low-pressure downstream section (2). Three commonly used types of flowmeters are illustrated: the orifice meter, the nozzle meter, and the Venturi meter. The operation of each is based on the same physical principles— an increase in velocity causes a decrease in pressure. The difference between them is a matter of cost, accuracy, and how closely their actual operation obeys the idealized flow assumptions.

 

We assume the flow is horizontal steady, (z1=z2) inviscid, and incompressible between points (1) and (2). The Bernoulli equation becomes:



If we assume the velocity profiles are uniform at sections (1) and (2), the continuity equation can be written as:


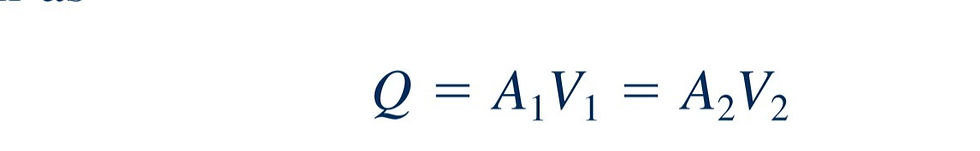
where is the small flow area at section (2). Combination of these two equations results in the following theoretical flowrate

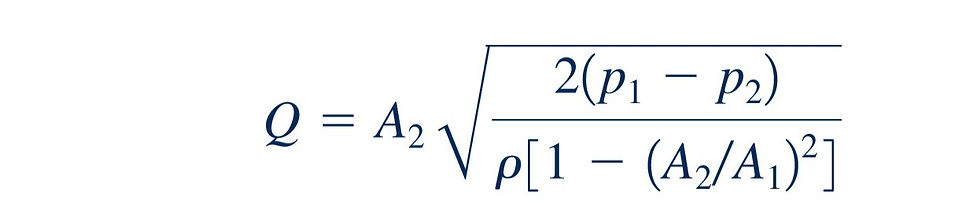
References📖

  1. Fundamentals of Fluid Mechanics by Bruce R. Munson 7th edition

  2. https://blog.craneengineering.net/what-is-pump-cavitation

  3. Introduction to Fluid mechanics/Edward J. Shaughnessy, Ira M. Katz, James P. Schaffer.

Additional Resources 🧪🔑

You can get deep insight about Process/Chemical Engineering from these sources😉:

  1. https://t.me/ebookgate/1127- Engineering Fluid Mechanics Book

  2. https://coursemania.xyz/course.html?id=433291- Free course on Fundamentals of Fluid Mechanics

  3. https://t.me/ebookstorage/178- Engineering Heat Transfer

  4. https://t.me/ebookstorage/159- Fundamentals of Engineering Thermodynamics (9th Edition) (2018)

  5. https://t.me/ebookstorage/183-Heat Transfer applications and principles

  6. https://t.me/ebookstorage/171-Design and Operation of Heat Exchangers and their Networks (2020)

  7. https://t.me/ebookstorage/215- Industrial Separation Processes (book)

  8. https://t.me/ebookstorage/214- Advanced Process Engineering Control (book)

  9. https://t.me/OilAndGas- Information about Oil&Gas (mainly arabic lang)

  10. https://t.me/chemical_worlds- Chemical Engineering Books, Quizzes and GATE Study Group

  11. https://t.me/chemical_environmental- Discussion group related to Chemical Engineering Problems

  12. https://t.me/chemicalengineeringworld_cew- Everything related to Chemical Engineering

  13. https://t.me/ebookgate- Chemical Engineering E-books (Telegram Channel)

  14. https://www.youtube.com/channel/UCqioh32NOJc8P7cPo3jHrbg- Piping Analysis

  15. https://www.youtube.com/channel/UCQfMyugsjrVUWU0v_ZxQs2Q -Mechanics of engineered devices

  16. http://chemicalengineeringguy.com/- suggests a wide range of courses in Chemical engineering (you can find free courses on topic of Aspen HYSYS, Aspen Plus)

  17. https://www.youtube.com/user/LearnEngineeringTeam- suggests working principles of every engineered devices, equipment and etch.

  18. https://www.youtube.com/channel/UCR0EfsRZIwA5TVDaQbTqwEQ- suggests great information about pumps, compressors with animation.


Today we have resumed learning about Fluid Dynamics part 2. Now, time to say goodbye👋🏻 until tomorrow and Stay tuned for more content 😉🌝✨!


✏️Note: If you need one of those books or links, you can contact me via my email or LinkedIn profile.

43 views0 comments

Recent Posts

See All

Comments

Post: Blog2_Post
bottom of page