top of page
Search
Writer's pictureTaliya Mammadhasanzada
Aug 16, 20206 min read

Fluid Statics 1

Warm greetings to all 🤩 in the 14th post on #Day13 ! Today, we begin to learn about Fluid Statics🦥. In this series of posts, we will learn about:

  1. Pressure at a Point,

  2. Basic Equation for Pressure Field,

  3. Pressure Variation in a Fluid at Rest,

  4. Incompressible Fluid and Compressible Fluid,

  5. Measurement of Pressure,

  6. Manometry, Piezometer Tube, U-Tube Manometer, Inclined-Tube Manometer,

  7. Mechanical and Electronic Pressure, Measuring Devices, Hydrostatic Force on a Plane Surface and etch.

Here we go 🦡,

Pressure at a Point🧩

The term pressure is used to indicate the normal force per unit area at a given point acting on a given plane within the fluid mass of interest. A question that immediately arises is how the pressure at a point varies with the orientation of the plane passing through the point. To answer this question, consider the free-body diagram, illustrated in Fig. 2.1,



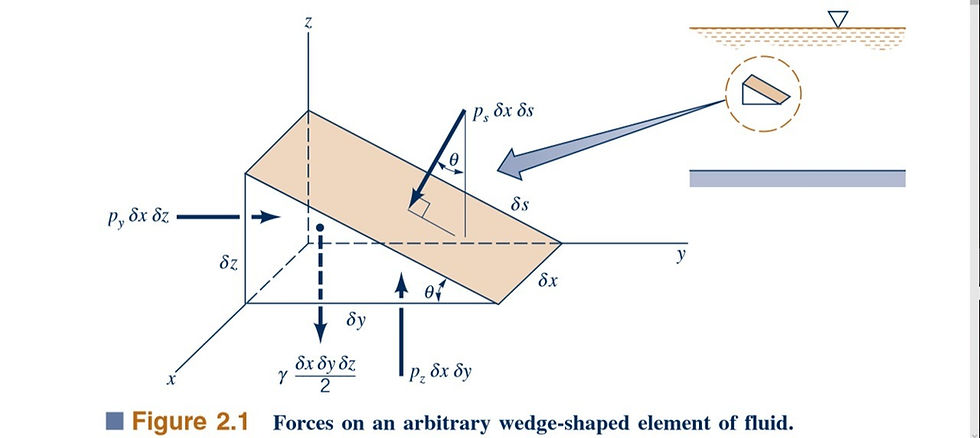
that was obtained by removing a small triangular wedge of fluid from some arbitrary location within a fluid mass. Since we are considering the situation in which there are no shearing stresses, the only external forces acting on the wedge are due to the pressure and the weight. For simplicity the forces in the x direction are not shown, and the z axis is taken as the vertical axis so the weight acts in the negative z direction. Although we are primarily interested in fluids at rest, to make the analysis as general as possible, we will allow the fluid element to have accelerated motion. The assumption of zero shearing stresses will still be valid as long as the fluid element moves as a rigid body; that is, there is no relative motion between adjacent elements. The equations of motion (Newton’s second law), in the y and z directions are, respectively

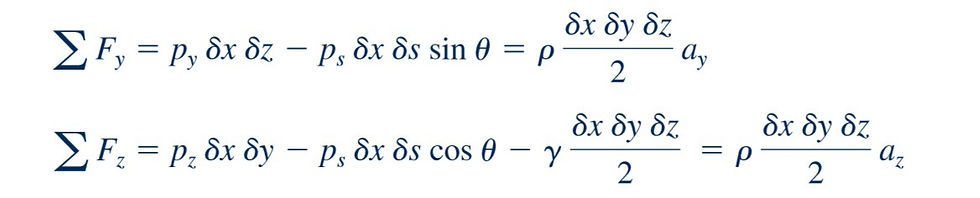
Geometrically, so that the equations of motion can be rewritten as


The angle was arbitrarily chosen so we can conclude that the pressure at a point in a fluid at rest, or in motion, is independent of direction as long as there are no shearing stresses present. This important result is known as Pascal’s law, named in honor of Blaise Pascal, a French mathematician who made important contributions in the field of hydrostatics. Thus, in this photo below at the junction of the side and bottom of the beaker, the pressure is the same on the side as it is on the bottom.


Basic Equation for Pressure Field🧩

Incompressible Fluid🧩

Since the specific weight is equal to the product of fluid density and acceleration of gravity changes in are caused by a change in density either or gravity acceleration g. For most engineering applications the variation in g is negligible, so our main concern is with the possible variation in the fluid density. In general, a fluid with constant density is called an incompressible fluid. For liquids the variation in density is usually negligible, even over large vertical distances, so that the assumption of constant specific weight when dealing with liquids is a good one. For this instance, Eq. 2.4 can be directly integrated

shows that in an incompressible fluid at rest the pressure varies linearly with depth. The pressure must increase with depth to “hold up” the fluid above it. It can also be observed from Eq. 2.6 that the pressure difference between two points can be specified by the distance h since


In this case h is called the pressure head and is interpreted as the height of a column of fluid of specific weight required to give a pressure difference.

Compressible Fluid🧩

We normally think of gases such as air, oxygen, and nitrogen as being compressible fluids because the density of the gas can change significantly with changes in pressure and temperature. Thus, although Eq. 2.4 (look at above) applies at a point in a gas, it is necessary to consider the possible variation in before the equation can be integrated. However, as was discussed, the specific weights of common gases are small when compared with those of liquids.

Since the specific weights of gases are comparatively small, it follows from Eq. 2.4 that the pressure gradient in the vertical direction is correspondingly small, and even over distances of several hundred feet the pressure will remain essentially constant for a gas. This means we can neglect the effect of elevation changes on the pressure for stationary gases in tanks, pipes, and so forth in which the distances involved are small.


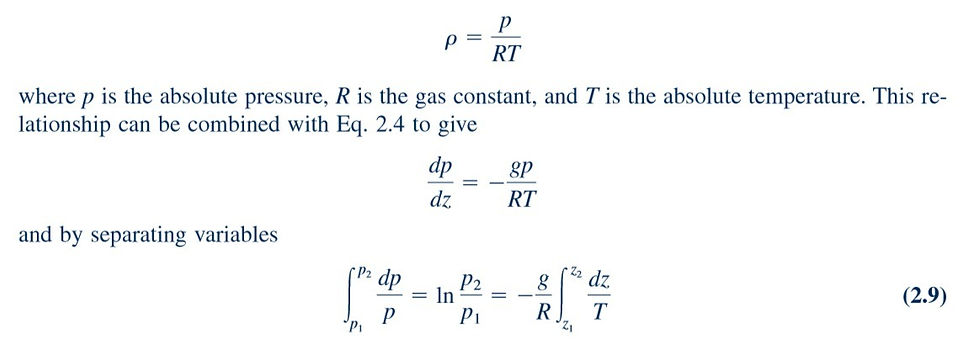
where g and R are assumed to be constant over the elevation change from Although the acceleration of gravity, g, does vary with elevation, the variation is very small. Before completing the integration, one must specify the nature of the variation of temperature with elevation. For example, if we assume that the temperature has a constant value over the range (isothermal conditions), it then follows from Eq. 2.9 that


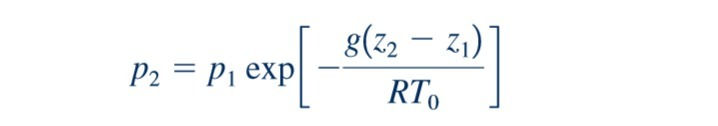
This equation provides the desired pressure–elevation relationship for an isothermal layer. As shown in the margin figure, even for a 10,000-ft altitude change, the difference between the constant temperature (isothermal) and the constant density (incompressible) results is relatively minor.

Measurement of Pressure🧩

Since pressure is a very important characteristic of a fluid field, it is not surprising that numerous devices and techniques are used in its measurement. The pressure at a point within a fluid mass will be designated as either an absolute pressure or a gauge pressure. Absolute pressure is measured relative to a perfect vacuum (absolute zero pressure), whereas gauge pressure is measured relative to the local atmospheric pressure. Thus, a gauge pressure of zero corresponds to a pressure that is equal to the local atmospheric pressure. Absolute pressures are always positive, but gauge pressures can be either positive or negative depending on whether the pressure is above atmospheric pressure (a positive value) or below atmospheric pressure (a negative value). A negative gauge pressure is also referred to as a suction or vacuum pressure. For example, 10 psi (abs) could be expressed as psi (gauge), if the local atmospheric pressure is 14.7 psi, or alternatively 4.7 psi suction or 4.7 psi vacuum.

The concept of gauge and absolute pressure is illustrated graphically in Fig. 2.7 for two typical pressures located at points 1 and 2.


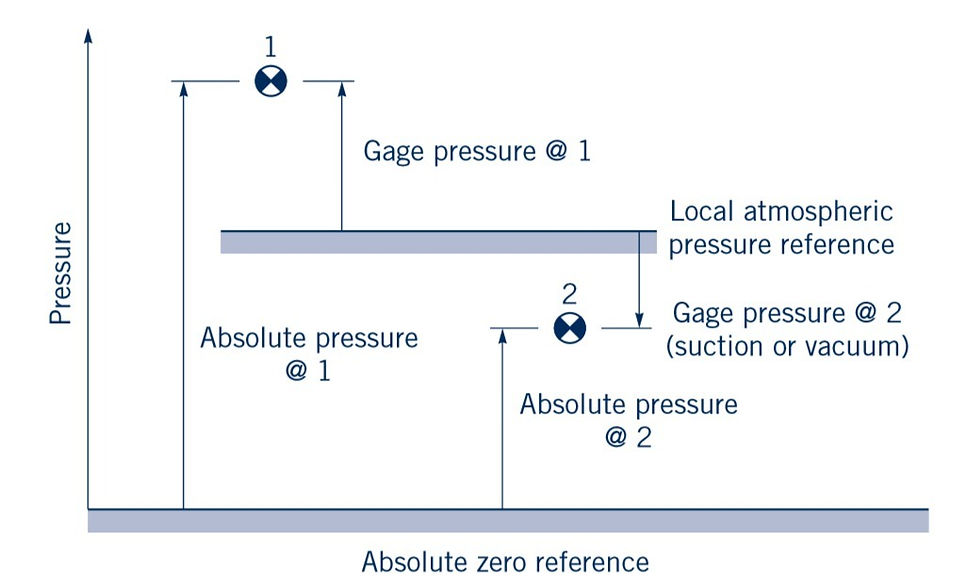
In addition to the reference used for the pressure measurement, the units used to express the value are obviously of importance. Pressure is a force per unit area, and the units in the BG system are or commonly abbreviated psf or psi, respectively. In the SI system the units are this combination is called the pascal and written as Pa. As noted in the beginning, pressure can also be expressed as the height of a column of liquid. Then the units will refer to the height of the column (in., ft, mm, m, etc.). For example, standard atmospheric pressure can be expressed as 760 mm Hg (abs). Generally, when we solve problems, pressures will be assumed to be gauge pressures unless specifically designated absolute. For example, 10 psi or 100 kPa would be gauge pressures, whereas 10 psia or 100 kPa (abs) would refer to absolute pressures.

It is noted that pressure differences are independent of the reference, so that no special notation is required in this case. The measurement of atmospheric pressure is usually accomplished with a mercury barometer, which in its simplest form consists of a glass tube closed at one end with the open end immersed in a container of mercury as shown in Fig. 2.8.

The tube is initially filled with mercury (inverted with its open end up) and then turned upside down (open end down), with the open end in the container of mercury. The column of mercury will come to an equilibrium position where its weight plus the force due to the vapor pressure (which develops in the space above the column) balances the force due to the atmospheric pressure. Thus:


References📖

  1. Fundamentals of Fluid Mechanics by Bruce R. Munson 7th edition

  2. Introduction to Fluid mechanics/Edward J. Shaughnessy, Ira M. Katz, James P. Schaffer.

Additional Resources 🧪🔑

You can get deep insight about Process/Chemical Engineering from these sources😉:

  1. https://t.me/ebookstorage/159- Fundamentals of Engineering Thermodynamics (9th Edition) (2018)

  2. https://t.me/ebookstorage/183-Heat Transfer applications and principles

  3. https://t.me/ebookstorage/171-Design and Operation of Heat Exchangers and their Networks (2020)

  4. https://t.me/ebookstorage/215- Industrial Separation Processes (book)

  5. https://t.me/ebookstorage/214- Advanced Process Engineering Control (book)

  6. https://t.me/OilAndGas- Information about Oil&Gas (mainly arabic lang)

  7. https://t.me/chemical_worlds- Chemical Engineering Books, Quizzes and GATE Study Group

  8. https://t.me/chemical_environmental- Discussion group related to Chemical Engineering Problems

  9. https://t.me/chemicalengineeringworld_cew- Everything related to Chemical Engineering

  10. https://t.me/ebookgate- Chemical Engineering E-books (Telegram Channel)

  11. https://www.youtube.com/channel/UCqioh32NOJc8P7cPo3jHrbg- Piping Analysis

  12. https://www.youtube.com/channel/UCQfMyugsjrVUWU0v_ZxQs2Q -Mechanics of engineered devices

  13. http://chemicalengineeringguy.com/- suggests a wide range of courses in Chemical engineering (you can find free courses on topic of Aspen HYSYS, Aspen Plus)

  14. https://www.youtube.com/user/LearnEngineeringTeam- suggests working principles of every engineered devices, equipment and etch.

  15. https://www.youtube.com/channel/UCR0EfsRZIwA5TVDaQbTqwEQ- suggests great information about pumps, compressors with animation.



Today we have already started learning about Fluid Mechanics part 1. Now, time to say goodbye👋🏻 until tomorrow and Stay tuned for more content 😉🌝✨!


✏️Note: If you need one of those books or links, you can contact me via my email or LinkedIn profile.


76 views0 comments

Recent Posts

See All

Comments

Post: Blog2_Post
bottom of page