Warm greetings 🤩to all in 12th 🦜post on #Day11 ! Today, we will continue and plan to finish the properties of Fluid. Here we go 🦅,
Bulk Compressibility Modulus👾
When a fluid is subjected to a pressure increase, the volume decreases, and the density increases. For many fluids the pressure–volume relationship is linear and may be characterized by a proportionality constant called the bulk compressibility modulus, E(v)📌. The relationship between a change in pressure, dp, and the corresponding fractional change in specific volume, dυ/υ, is written in terms of E(v) as:
dp=−E(v)*dυ/υ
The minus sign is necessary because a positive change in pressure (a pressure increase) results in a negative change in volume (a volume decrease). Since
−dυ/υ =dρ/ρ then
dp=E(v)*dρ/ρ
This equation can be rearranged to define the bulk modulus as
📌E(v)=dp/(dρ/ρ)
Since dρ/ρ is a dimensionless ratio, the dimensions and common units for E(v) are the same as those for pressure, {FL^(−2)}, and thus pascals or psi.
For gases, the precise value of the bulk modulus depends on the type of compression process which occurs. For a perfect (ideal) gas undergoing an isothermal process
dp= R*T(0)*dρ.
Thus the isothermal bulk modulus of a perfect gas can be written as
E(v) = dp/(dρ/ρ) = R*T(0)*dρ*(dρ/ρ) = ρ*R*T(0) = p
and we can write the isothermal bulk modulus of a perfect gas in two ways:
E(v) = ρ*R*T(0)
E(v) = p
If a perfect gas undergoes an isentropic (frictionless and without heat transfer to the surroundings) process, then it can be shown that the isentropic bulk modulus is given by
📌E(v) = γp
A material with a large value of the bulk modulus, i.e., a liquid or solid, undergoes a negligible change in density when exposed to the highest pressures normally encountered in engineering. Such materials are incompressible. For example, a pressure increase of over 3100 psi is required to increase the density of water by 1%. Since liquids are virtually impossible to compress by using reasonable pressures, we will assume that a liquid has a constant density unless otherwise noted.
Viscosity🧯
In our discussion of Flow of Fluid 2 of the basic characteristics of fluids and solids, the viscosity of a fluid, µ, was defined as the constant of proportionality between shear stress and the transverse velocity gradient. In fluid mechanics the viscosity µ is referred to as the absolute or dynamic viscosity, but a more descriptive name is shear viscosity. Figure 2.17
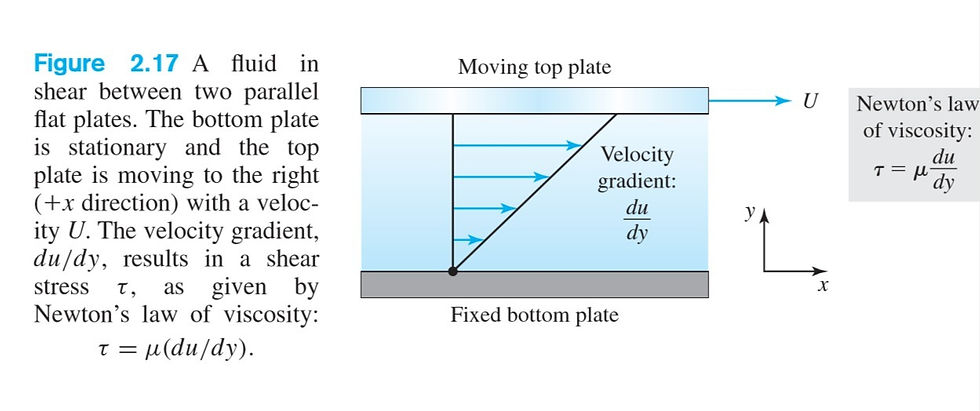
shows a thin layer of fluid being sheared between two closely spaced parallel flat plates. This geometry models the lubricant-filled space between a piston and cylinder wall in an engine, in a journal bearing, or between your foot and the wet floor in your bathroom.
📌Note the linear velocity profile within the fluid layer, and note also that at both fluid–solid interfaces the fluid velocity matches the velocity of the solid surface. The latter condition, which is virtually always satisfied, is known as the no-slip condition. The no-slip condition reflects the fact that there is a thin layer of fluid adsorbed (held by molecular forces) to a solid surface. The first consequence of fluid viscosity is a resistance to shear in accordance with Newton’s law of viscosity
τ = µ*(du/dy)
🔌The shear viscosity of a fluid is a strong function of temperature but only a weak function of pressure. The temperature dependence of viscosity differs for liquids and gases. Shear viscosity increases with temperature for gases but decreases with temperature for liquids. To understand the temperature dependence of viscosity, we must consider the mechanisms by which momentum is transferred in fluids.
⚙️In liquids the viscosity, or ability to transfer momentum, is a result of the intermolecular attractive forces between adjacent molecules. As the temperature increases, the strength of this cohesive force decreases, and the average separation distance between liquid molecules increases. The liquid transfers momentum less effectively, so viscosity decreases.
🕯In gases, molecules are not close enough together for intermolecular forces to be important. The mechanism responsible for momentum transfer is fundamentally different. Gas molecules are far more mobile than those in a liquid. Some of these energetic gas molecules move in a direction with a component perpendicular to the motion of the top plate. The molecules moving from the “fast” fluid layer to the “slower” moving layer below act to pull the “slower” layer forward. In contrast, the molecules moving from the “slower” layer to the “faster” layer exert a drag on the “faster” layer. Since a rise in temperature increases the random molecular motion in all directions (including the perpendicular direction), the shear viscosity of a gas increases with rising temperature.
🧐Suppose you are asked to predict the temperature of minimum shear viscosity for water in the temperature range 50–150◦C. To do so, you must recognize that water undergoes a liquid–gas phase change in this temperature range. First consider the temperature dependence of viscosity for the liquid phase. Viscosity decreases with increasing temperature in a liquid, so the minimum viscosity for the liquid phase occurs at a temperature just below the boiling point. In contrast, the viscosity of a gas increases with increasing temperature, so the minimum viscosity for the gas phase occurs just above the boiling temperature. The viscosity of steam is always less than that of water, so the minimum viscosity for H2O over the range 50–150◦C must occur in the vapor phase just above the boiling temperature. A different way to express the shear viscosity is to divide it by the density. This normalized form, called the kinematic viscosity, ν, is defined as:
ν = µ/ρ
The dimensions of kinematic viscosity are expressed in units of m2/s, or ft2/s.
Surface Tension🤖
🤨Perhaps you have wondered why a sponge soaks up water so readily, whereas the treated fabric of a raincoat is impervious to water. Water forms a thin film on a clean windshield, but it beads on the same surface after the use of a windshield treatment. Water also beads on a waxed or oily automobile surface, but when a little detergent is added, it will spread into a thin film. A jet of water tends to break up into a spray of small spherical droplets.
🧩Liquids may either advance up a small tube against the force of gravity or stubbornly refuse to enter the tube at all. These are all examples of surface tension phenomena. What is responsible at the molecular level for the variety of behaviors associated with the presence of an interface between two fluids? Let's look at this picture example (Fig 2.19):
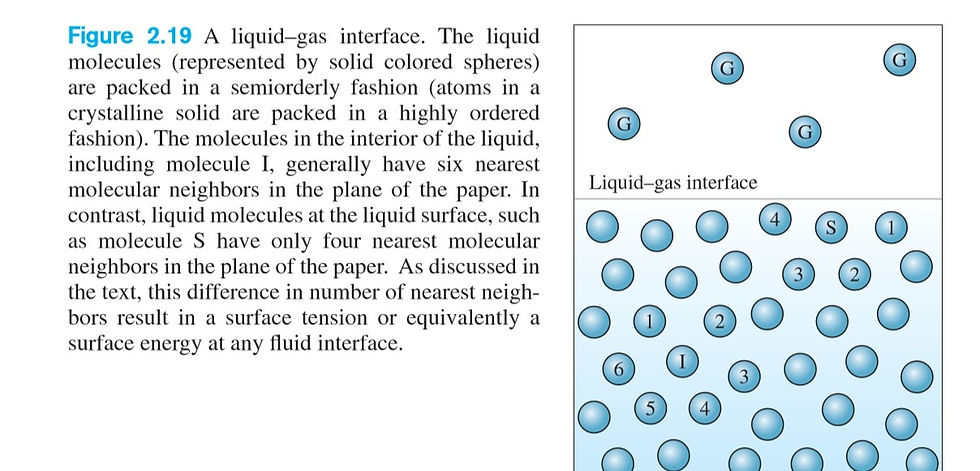
Molecules below the surface of a liquid have a characteristic number of nearest neighbors. The total energy of the fluid system is minimized when each molecule has the “correct” number of neighbors (determined by the bonding characteristics of the atoms in the fluid). Molecules at the liquid surface, however, have a different number of nearest neighbors. There are two ways to interpret this observation. First, since the surface molecules have the “wrong” number of neighbors, they will be at a higher energy state. The excess energy associated with the molecules at the surface is known as surface energy. Surface energy, which is represented by the symbol σ, has dimensions of energy per unit area.
A different but equivalent model for a liquid–vapor interface recognizes that since the surface molecules of liquid do not have identical molecules above them, they will be more strongly attracted to their neighbors below and in the plane of the interface. The result is a layer of surface molecules that at the macroscopic level behaves as an elastic membrane. The corresponding net force on a molecule in the interface acts in the plane of the surface in all directions and is referred to as the surface tension (see Figure 2.20).
Surface tension has dimensions of force/length, which is dimensionally equivalent to surface energy. The units for surface tension are N/m, dyn/cm, or lbf/ft. We will use the concept of surface tension in the remainder of this section, but note that both approaches (surface tension and energy) are valid ways to investigate interfacial phenomena.
🎬The magnitude of the surface tension is a function of the fluids on both sides of the interface. Thus, the surface tension at an air–water interface is different from that at an oil–water interface. The influence of both fluids on the surface tension is a reflection of the fact that atoms in the second fluid are serving as substitute nearest neighbors for the surface atoms in the first fluid and vice versa.
Pressure Jump Across a Curved Interface 🍹
⛳️To see how the concept of surface tension is used to analyze a practical problem, consider a small spherical drop of one fluid at rest in another, such as a tiny fuel droplet in the vicinity of a fuel injection nozzle. Since the drop is small, we can neglect the slight hydrostatic pressure variation with height and assume a uniform but different pressure inside and outside the drop. Imagine cutting the drop in half as shown in Figure 2.21 and
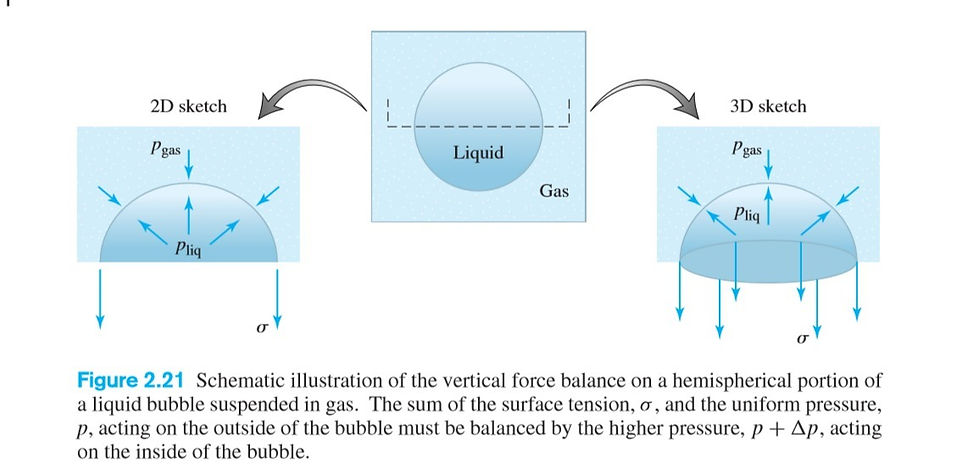
performing a force balance in the vertical direction on the hemispherical interface.If the drop is at rest, then Newton’s second law tells us that the sum of the forces acting on the interface in any direction must be zero. The only forces acting on the interface are those due to pressure and surface tension. The interface itself is infinetely thin and mass less. Equilibrium requires that the net force up due to pressure inside, plus the net force down due top pressure outside, plus the surface tension force pulling down on the edge of the hemispherical interface, add to zero. The net action of a uniform pressure inside a hemisphere is as if the same pressure acted on the equatorial plane of area π*r^2. Surface tension acts on the circumference of the hemisphere, 2*π*r. If we let delta p be the pressure difference, inside minus outside, then the force equilibrium condition just stated becomes
delta p(π*r^2) = σ(2*π*r)
Solving for the pressure difference (jump) across the interface yields
delta p =2σ/r
This result shows that surface tension causes the pressure inside a drop or bubble to be greater than the pressure outside. Smaller drops and bubbles experience larger pressure differences, and for a given drop or bubble size, a higher surface tension value produces a larger pressure differences.
References 📖
Introduction to fluid mechanics/Edward J. Shaughnessy, Ira M. Katz, James P. Schaffer.
Additional Resources 🧪🔑
You can get deep insight about Process/Chemical Engineering from these sources😉:
https://t.me/ebookstorage/171-Design and Operation of Heat Exchangers and their Networks (2020)
https://t.me/ebookstorage/215- Industrial Separation Processes (book)
https://t.me/ebookstorage/214- Advanced Process Engineering Control (book)
https://t.me/OilAndGas- Information about Oil&Gas (mainly arabic lang)
https://t.me/chemical_worlds- Chemical Engineering Books, Quizzes and GATE Study Group
https://t.me/chemical_environmental- Discussion group related to Chemical Engineering Problems
https://t.me/chemicalengineeringworld_cew- Everything related to Chemical Engineering
https://t.me/ebookgate- Chemical Engineering E-books (Telegram Channel)
https://www.youtube.com/channel/UCqioh32NOJc8P7cPo3jHrbg- Piping Analysis
https://www.youtube.com/channel/UCQfMyugsjrVUWU0v_ZxQs2Q -Mechanics of engineered devices
http://chemicalengineeringguy.com/- suggests a wide range of courses in Chemical engineering (you can find free courses on topic of Aspen HYSYS, Aspen Plus)
https://www.youtube.com/user/LearnEngineeringTeam- suggests working principles of every engineered devices, equipment and etch.
https://www.youtube.com/channel/UCR0EfsRZIwA5TVDaQbTqwEQ- suggests great information about pumps, compressors with animation.
🔌Today we have continued to learn about Fluid Mechanics, mainly focused on Fluid Properties 2. Tomorrow, we will finish Fluid Properties with Surface Tension, Wetting, Capillary action and Fluid Energy. Now, time to say goodbye👋🏻 until tomorrow and Stay tuned for more content 😉🌝✨!
✏️Note: If you need one of those books or links, you can contact me via my email or LinkedIn profile.
#process #processengineering #engineering #chemical #chemicalengineering #technical #education #dailypost #newpost #wixsite #day11 #technology #material #materialbalance #mass #massbalance #project #projectengineering #selfdevelopment #challenge #recycle #streams #purge #improvement #fluidflow #flow #fluidmechanics #fluiddynamics #water #waterhammer #contuinity #energy #equations #Pfd #processdiagrams #diagrams #piping #instrumentation #pid #development #examples #study #studentlife
Коментарі