Fluid Mechanics (Properties of Fluid 3)🧩
- Taliya Mammadhasanzada

- Aug 15, 2020
- 6 min read
Warm greetings to all🤩 in the 13th post on #Day12 ! Today, we will complete the properties of fluid 3 in Fluid Mechanics. Here we go🤿,
Capillary Action⚙️
Let's consider what happens if a thin glass tube is inserted into a liquid. If the liquid wets the glass, it will enter the tube by capillary action. If the liquid does not wet the glass, it will be prevented from entering the tube. Both effects are due to surface tension. Let us analyze the case in which a liquid wets a round tube with a contact angle θc as shown in Figure 2.23C.
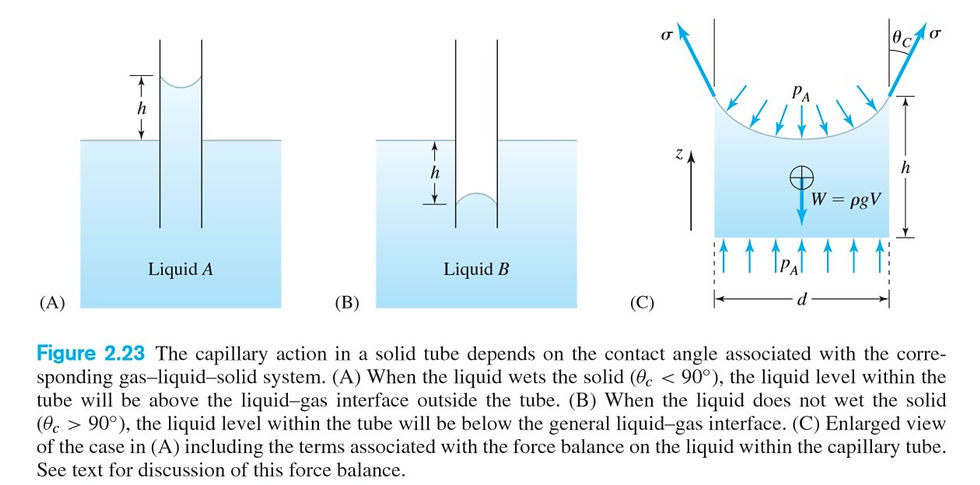
The liquid will be drawn up a tube of diameter d to a height h. We will perform a force balance in the z direction on the column of liquid shown in Figure 2.23C, taking into account surface tension, gravity, and pressure. The column is at rest, so the sum of all forces acting on the fluid column is zero. The pressure acting on the top of the meniscus formed in the tube is atmospheric. The pressure acting at the bottom of the liquid column inside the tube is also atmospheric, because lines of constant pressure in a stationary fluid in a gravity field are horizontal,and the tube is open. We are neglecting the tiny change in atmospheric pressure over the height of the liquid column. 🍹Since atmospheric pressure acts over an area equal to the cross section of the tube at each end, the net effect of pressure on the liquid column is zero. The surface tension force acting up on the contact line, plus the force of gravity on the liquid column acting down must therefore add to zero. From the geometry at the contact line we find
σπd cosθc −π*((d^2)/4)*ρgh=0
Solving for the height of capillary rise, we have
h =4σ*cosθc/dρg
📌Capillary action is often cited as causing the movement of fluid from the roots of a plant to its crown where the leaves are present. In Sequoia redwood trees, the capillary rise would have to exceed 200 ft. This seems unlikely. Alternate theories argue that the minute water columns in the trees’ tissues are in a state of tension (otherwise normally prohibited) caused by evaporation at the leaf surface. Capillary action also explains the tendency of liquids to penetrate cracks even when there is no differential pressure acting to drive the liquid into the cracks. A two dimensional model for the rise of a liquid in a crack of width w is shown in Figure 2.24.

A force balance indicates that the height of the rise of a liquid in a crack which it wets is given by
h =2σ*cosθc/wρg
Notice that the height to which a liquid rises in a round tube of diameter d is twice the height to which the same liquid rises in a crack of width w =d.
Types of Fluid Energy🧯
⛳️Kinetic energy:
The energy associated with fluid in motion is called kinetic energy, E(k). This energy is proportional to the mass of fluid in the system, and to the square of the fluid speed, v. For a mass of fluid m, the total kinetic energy is given by
E(k) = 1/2*m*(v^2)
The corresponding kinetic energy per unit mass is
e(k) = 1/2*(v^2)
while kinetic energy per unit volume is given by:
ρ*e(k) = 1/2*ρ*(v^2)
⛳️Potential energy:
A second form of potential energy is related to the ability of fluid at high pressure to perform mechanical work. The pressure potential energy E(p) of a mass m of fluid is given by
E(p) = m*p/ρ = p*V
where V is the volume of the fluid, and pressure is measured with respect to the ambient pressure at which spent fluid is exhausted. The per-unit-mass form of this potential energy is
e(p) = p/ρ
with the per-unit-volume counterpart being:
ρ*e(p) = p
⛳️Total energy:
The total energy E of a mass of fluid M can be represented as the sum of its internal, kinetic, and two types of potential energy as
E =U + 1/2*m*(v^2) +m*g*z+m*p/ρ
In engineering applications it is the change in total energy that is important rather than an absolute value. On a per-unit-mass basis, total energy is given by
e =u+1/2*(v^2)+g*z+p/ρ
and on a per-unit-volume basis we have:
ρ*e = ρ(u+1/2*(v^2)+g*z+p/ρ)
The sum: 1/2*(v^2)+g*z+p/ρ is usually referred to as the mechanical energy per unit mass, and it is this energy that is turned into internal energy by the action of viscosity and lost.
Summary 🤖
These 3 posts serve as an introduction to the fluid and flow properties needed to specify the dynamic and thermodynamic state of a fluid. The mass of an object is defined as a measure of its resistance to acceleration, and its weight is the magnitude of the force acting on the object due to gravity. Properties that depend on the amount of fluid in a system are termed extensive properties. If an extensive property is divided by the total mass or the total volume of the fluid, the result is an intensive property. For example, we will make frequent use of the fluid density defined as the mass of a fluid divided by its volume. The local density is defined by the conditions of pressure and temperature existing in the fluid at that point. Specific gravity is defined as the ratio of a fluid’s density to that of a standard reference fluid (usually water or air) at STP.
⛳️Pressure
is the compressive normal component of the force applied by a fluid to a surface, divided by the area of that surface. Absolute pressure is defined in reference to a perfect vacuum, while gauge pressure is specified with reference to atmospheric or ambient pressure. Pressure differences can cause a fluid to flow or be caused by a fluid flow. Archimedes’ principle defies the magnitude and direction of the buoyancy force acting on an object immersed in a stationary fluid.
⛳️The buoyancy force
acts in the direction opposite to that of the gravitational force and has a magnitude equal to the weight of the displaced fluid.
⛳️The temperature
of a fluid is a thermodynamic state variable that provides a measure of the internal energy stored in the fluid. In a fluid in equilibrium, the temperature is proportional to the mean kinetic energy of the random motion of the molecules. Temperature differences may create a fluid flow, or they may be a consequence of a fluid flow. Temperature differences in a fluid are always accompanied by the flow of heat by molecular conduction. The relationship between heat flux, temperature gradient, and thermal conductivity is given by Fourier’s law of heat conduction.
⛳️Compressibility
For many fluids the pressure–volume relationship is linear and characterized by a constant of proportionality called the bulk compressibility modulus. Fluids of large compressibility modulus (liquids) undergo negligible changes in density when subjected to even the largest pressures encountered in engineering, making them effectively incompressible.
⛳️Viscosity
The shear viscosity can also be interpreted as the constant of proportionality between the velocity gradient and the momentum transfer rate. The shear viscosity of a fluid is a strong function of temperature but a weak function of pressure. It increases with temperature for gases but decreases with temperature for liquids. An important consequence of the existence of a shear viscosity in a fluid is that of viscous dissipation or loss of energy when a fluid is sheared.
⛳️Surface tension
The extra energy associated with the molecules at the surface of a fluid is known as the surface energy. The corresponding net force on a molecule in the surface layer acts in the plane of the surface in all directions and is referred to as the surface tension. Surface tension causes the pressure inside a fluid drop to be greater than the pressure outside, and since the delta p is inversely related to the size of the bubble, smaller bubbles experience larger pressure differences. Surface tension is an important factor in a variety of fluid phenomena including capillary action, the waterproofing of fabric, and the cleaning action of soaps and detergents.
⛳️Energy
A fluid contains internal, kinetic, and potential energy. Significant changes in the energy content of a fluid are important in many applications including those in which the fluid performs work and those in which work is done on the fluid. The various forms of energy in a fluid can be considered to be extensive quantities or on a per-unit-mass or per-unit-volume basis.
References 📖
Introduction to fluid mechanics/Edward J. Shaughnessy, Ira M. Katz, James P. Schaffer.
Additional Resources 🧪🔑
You can get deep insight about Process/Chemical Engineering from these sources😉:
https://t.me/ebookstorage/183-Heat Transfer applications and principles
https://t.me/ebookstorage/171-Design and Operation of Heat Exchangers and their Networks (2020)
https://t.me/ebookstorage/215- Industrial Separation Processes (book)
https://t.me/ebookstorage/214- Advanced Process Engineering Control (book)
https://t.me/OilAndGas- Information about Oil&Gas (mainly arabic lang)
https://t.me/chemical_worlds- Chemical Engineering Books, Quizzes and GATE Study Group
https://t.me/chemical_environmental- Discussion group related to Chemical Engineering Problems
https://t.me/chemicalengineeringworld_cew- Everything related to Chemical Engineering
https://t.me/ebookgate- Chemical Engineering E-books (Telegram Channel)
https://www.youtube.com/channel/UCqioh32NOJc8P7cPo3jHrbg- Piping Analysis
https://www.youtube.com/channel/UCQfMyugsjrVUWU0v_ZxQs2Q -Mechanics of engineered devices
http://chemicalengineeringguy.com/- suggests a wide range of courses in Chemical engineering (you can find free courses on topic of Aspen HYSYS, Aspen Plus)
https://www.youtube.com/user/LearnEngineeringTeam- suggests working principles of every engineered devices, equipment and etch.
https://www.youtube.com/channel/UCR0EfsRZIwA5TVDaQbTqwEQ- suggests great information about pumps, compressors with animation.
Today we have already finished learning about Properties of Fluid 3. Now, time to say goodbye👋🏻 until tomorrow and Stay tuned for more content 😉🌝✨!
✏️Note: If you need one of those books or links, you can contact me via my email or LinkedIn profile.
#process #processengineering #engineering #chemical #chemicalengineering #technical #education #dailypost #newpost #wixsite #day12 #technology #material #materialbalance #mass #massbalance #project #projectengineering #selfdevelopment #challenge #recycle #streams #purge #improvement #fluidflow #flow #fluidmechanics #fluiddynamics #water #waterhammer #contuinity #energy #equations #Pfd #processdiagrams #diagrams #piping #instrumentation #pid #development #examples #study #studentlife





Comments